중학생이 되고 처음 배우는 개념인 함수는 상당히 접근하기 어렵다.
우선 사전적 정의를 보자

도저히 무슨 말인지 이해가 안간다.
아울러 함수는 영어로 Function 이다
함수를 약어로 F(x)를 사용하는 이유다!

수학에서 사용되는 용어들은 한자를 알고 이해하면 조금 이해하기 편하다


함수(函數)란? "나무로 짠 궤 + 숫자"
"나무로 짠 궤"는 아래와 같이 생겼다

예를 들어보자
어떤 숫자 "1"을 함수에 넣었을때 출력결과가 "2"가 나왔다
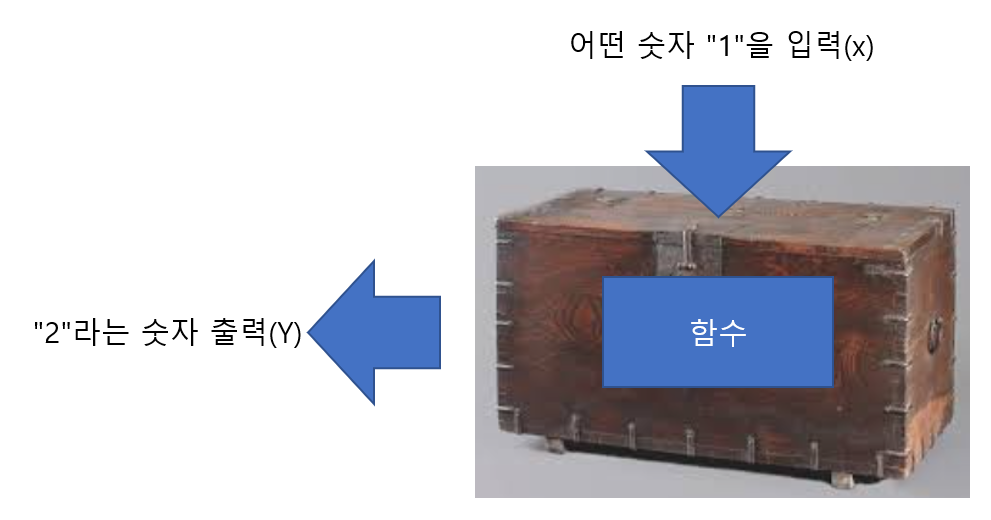
이를 다를게 표현하면

"출력" = "함수식"에 "x"라는 값을 입력한 값
"Y=f(x)" 라는 함수가 이해가 될것이다
예를 들어)
"Y = 2x" 라는 함수가 있다. 이 함수는 "Y= f(x) = 2x" 라 쓰기도 한다.
x = 1을 입력하면 출력 Y = 2가 되고
x = 2을 입력하면 출력 Y = 4가 되고
x = 3을 입력하면 출력 Y = 6가 되고
x = 4을 입력하면 출력 Y = 8가 되고
x = 5을 입력하면 출력 Y = 10가 되고..........
계속 쓰려니 상당히 귀찮다
그냥 "Y = 2x" 라 쓰면 편하다
그래프로 그리면 더 편하나 그래프는 공간을 많이 차지 한다
간단 명료하게 "Y=2x" 또는 "Y= f(x) = 2x"로 수학에서는 축약하여 표현하는 것을 좋아 한다
이것이 간단한 함수의 기초이다.

그리고 "Y= f(x) = 2x" 라는 함수를 그래프로 그려봤다.
함수는 필연 그래프를 동반하면 이해가 빠르다.
x에 들어갈 숫자는 1,2,3,4 같은 정수도 되지만 1.1, 1.2, 1.3 등등등...
여러 숫자를 넣을 수 있고, 이런 숫자들의 결과물의 집합 Y 값은 결국 선이 되게 된다.
그러므로 그래프가 그려지게 되므로 함수와 그래프는 별개의 개념이 아니다.
'[수학]' 카테고리의 다른 글
| [수학] 점,선,면 및 극한의 기초 (0) | 2021.01.19 |
|---|---|
| [수학 루트] 루트의 개념 2 (0) | 2021.01.17 |
| [그래프 그리기] desmos 사이트 소개 (0) | 2021.01.04 |
| [수학 루트의 개념] 제곱근 루트 개념1 (0) | 2019.05.15 |
| [수학, 지수의 개념] 지수의 개념 (0) | 2019.05.15 |