뭐라도 배우자

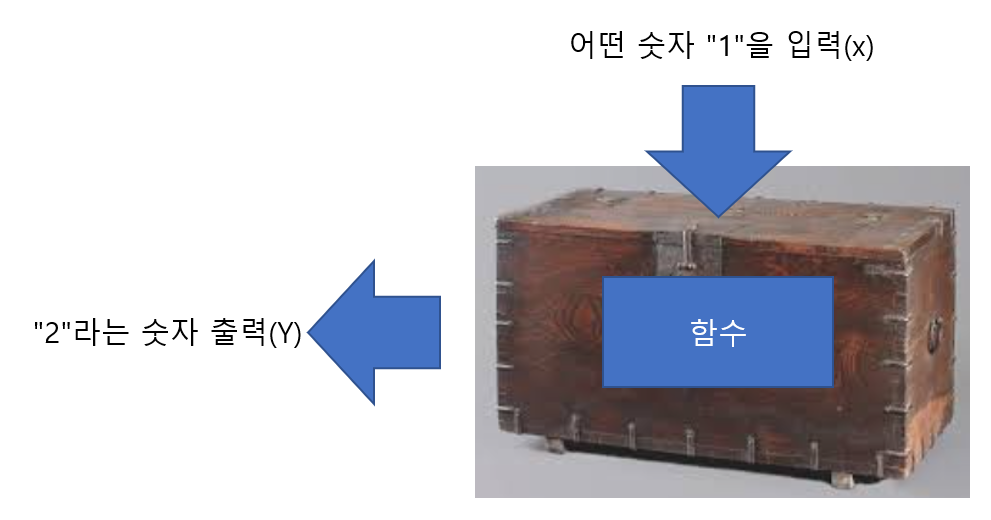
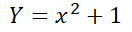적분은 크게 부정적분과 정적분으로 나누어지는데 
아래의 개념은 정적분의 개념입니다.

부정적분에 대한 부분은 추가 포스팅 예정입니다. - 23.03.06 by studyexcel

적분 積分 = 쌓을(적), 나눌(분)

적분이라는 어려운 단어에는
이미 그 해석이 나와 있다

“나누어서 쌓는다”는
개념 이다.

근데 왜 나누어서 쌓을까?
모가 좋길래?

1. 우리는 사각형의 넓이를
    구하는 방법을 잘 알고 있다

2. 아래와 같은 어려운? 면적의
    그래프의 넓이를 구하려면
     어떻게 해야할까?

3. 이런 특이한 면적을 구하기 위해
    적분의 개념이 필요하다

    적분("나누어 쌓는다") 의 발상으로
    아래와 같은 아이디어를 낼 수 있다

    1) 특이한 도형의 X축의 길이는
         편의상 “8”로 정한다

    2)  “0”과 “8“사이는 무한하게 많은
         숫자가 존재한다
         예를들어 1부터 숫자를 세면
          1, 1.1, 1.111,1.111 등 무한한 수가
          존재한다  

    3) 이렇게 무한한 숫자가
        존재하는 "X축"을 기준으로
        아주 작은 사각형을 무한개로
        특이한 도형을 채워 본다

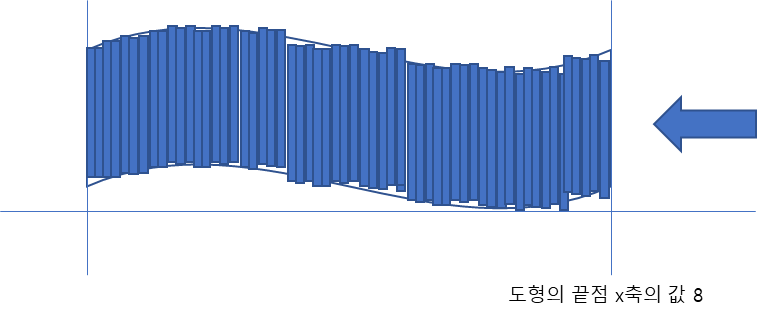
4) 특이한 도형을
    작은 사각형을 꽉채우고
   
    그려놓은 무한히 많은
    사각형은 "가로x세로" 방식으로
    "한개 사각형의 넓이를 구하고"

    이걸 모두 더하면?

    결론적으로 특이한? 도형의
    면적을 구할 수 있다
   
    자세히 보면 그래프에
    틈이 존재하는데 이는
    수학적으로 무시할 정도로
    작은 차이로 보면 된다
     무시하라는 뜻이다  

    5) 이게 적분의 개념이다
         ㄴ왜 미세하게 분해 해서
            쌓아야 하는지 알겠는가?

          결론적으로 특이한 도형의
          면적을 쉽게 구하고 싶어서
          라고 말하고 싶다

          세상은 사각형, 삼각형으로
           되어 있지 않은 많은 도형이
           존재하는데

           이를 단순화 하여(사각형으로
           만들어서..) 쌓아서 면적을
           구하기 위한게 적분이다         

4. 간단한 적분 수식을
     한번 보자

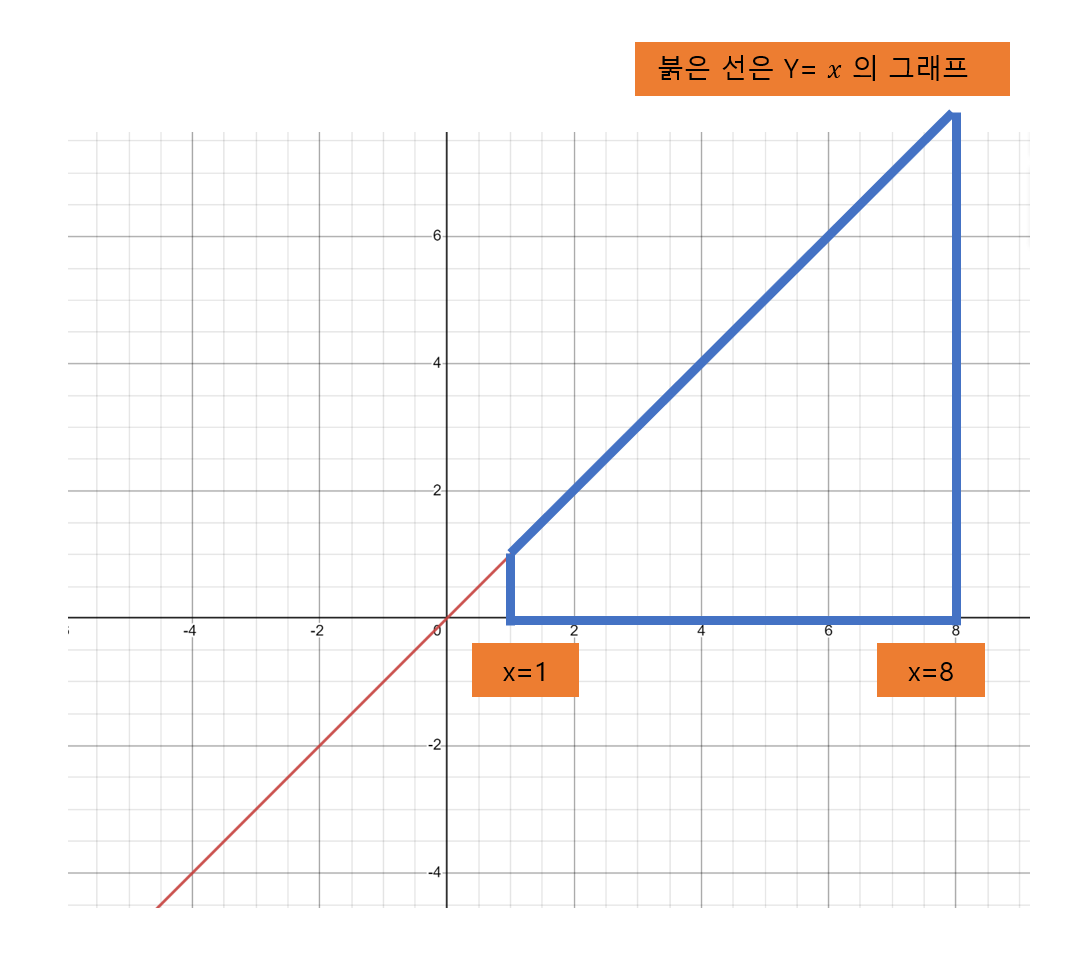
위와 와 같은 함수 Y= X 라는
그래프를 먼저 그리고, 
X축의 1~8 사이의 면적을 
구하라는 이야기다

쉽게 말해서 면적 구하라는
이야기이다

그래프를 그리면
좀 더 이해가 쉽다

아래 수식이 의미하는
바는 그래프의  파란선의
영역의 면적을
"나누어 쌓아서 (적분)해서"
넓이를 구하라는 뜻이다.

5. 적분 기호(인테그랄)를 벗어나는(?)
    규칙은 아래와 같다

6. 잘못적은 블로그 내용 수정요청은 언제든 환영합니다.

시그마를 사용하는 이유?
간단하게 표현하고 싶어서 라고 말하고 싶다

아래와 같이 더하기를 표현한다고 해보자..
1+2+3+4+5+6+7+ ~ +99+100
ㄴ 너무 길다 이걸 간단하게 표현하고 싶을땐?

위를 해석해보면 

K=1 부터 시작해서 100까지 증가되고,

씨그마는 더하기가 생략되어 있다

상당히 간단하게 표현이 가능하다

좀 더 응요하면

K=50 부터 시작해서

100까지 증가되고,

더하기가 생략 되어 있다

한번더 응용해보면 아래와 같이
표현 가능하다

함수가 들어갔다고 절대 겁먹지
말아라.. 그냥 K라는 곳에 1부터
5까지 넣고 풀어 쓰면 된다

시그마는 더하기가 내포되어
있음에 주의해서 적으면
아래와 같다

추가로 응용해보면 아래와 같다
K=1부터 5이고, 시그마는 더하기가 내포되어 있고, 
x는 크게 고민하지 않고 그냥 적으면 된다

숫자 "5"대신에 "m"이라는
상수를 넣을 수 도 있다

그럼 몇번 식을 더해야할까?

정답은 "m번"이다

m이 10이면 10개,
m이 100이면 100개의
식을 더하면 된다

아래의 경우는 어떻게 될까?
K=1 to 4는 결국 4개의
식이 만들어진다는 뜻

따라서 결과는
3+3+3+3 = 12가 된다

상기내용을 공식화 하면
아래와 같다

이해만 한다면 절대 공식을
외울 필요가 없다

점, 선, 면 기초를 알면..

이를 확장해서 무한대(극한)의

념을 이해 할 수 있게 된다

이를 잘 이해를 했다면 극한으로 확장을 할 바탕이 되었다.

극한은 다음회차에 ~

https://studyexcel.tistory.com/18

https://studyexcel.tistory.com/17

중학생이 되고 처음 배우는 개념인 함수는 상당히 접근하기 어렵다.

우선 사전적 정의를 보자

도저히 무슨 말인지 이해가 안간다.

아울러 함수는 영어로 Function 이다

함수를 약어로 F(x)를 사용하는 이유다!

수학에서 사용되는 용어들은 한자를 알고 이해하면 조금 이해하기 편하다

 함수(函數)란? "나무로 짠 궤 + 숫자"

"나무로 짠 궤"는 아래와 같이 생겼다

예를 들어보자

어떤 숫자 "1"을 함수에 넣었을때 출력결과가 "2"가 나왔다

이를 다를게 표현하면

"출력" = "함수식"에 "x"라는 값을 입력한 값

"Y=f(x)" 라는 함수가 이해가 될것이다

예를 들어)

"Y = 2x" 라는 함수가 있다. 이 함수는 "Y= f(x) = 2x" 라 쓰기도 한다.

x = 1을 입력하면 출력 Y = 2가 되고

x = 2을 입력하면 출력 Y = 4가 되고

x = 3을 입력하면 출력 Y = 6가 되고

x = 4을 입력하면 출력 Y = 8가 되고

        x = 5을 입력하면 출력 Y = 10가 되고..........

계속 쓰려니 상당히 귀찮다

그냥 "Y = 2x" 라 쓰면 편하다

그래프로 그리면 더 편하나 그래프는 공간을 많이 차지 한다

간단 명료하게 "Y=2x" 또는 "Y= f(x) = 2x"로 수학에서는 축약하여 표현하는 것을 좋아 한다

이것이 간단한 함수의 기초이다.

그리고 "Y= f(x) = 2x" 라는 함수를 그래프로 그려봤다.

함수는 필연 그래프를 동반하면 이해가 빠르다.

x에 들어갈 숫자는 1,2,3,4 같은 정수도 되지만 1.1, 1.2, 1.3 등등등...

여러 숫자를 넣을 수 있고, 이런 숫자들의 결과물의 집합 Y 값은 결국 선이 되게 된다.

그러므로 그래프가 그려지게 되므로 함수와 그래프는 별개의 개념이 아니다.

2021.01.04 - [[수학]] - [그래프 그리기] desmos 사이트 소개

함수(Function)을 잘 이해하려면 그래프에 익숙해야 한다.

2차원 그래프, 3차원그래프 등등 전부 함수를 베이스로 그릴 수 있는 그래프다.

웹사이트에서 손쉽게 그래프를 그릴 수 있는 사이트를 소개합니다.

www.desmos.com/calculator/zukjgk9iry?lang=ko

1. 목차를 눌러서 : 그래프의 형태를 선택한다

2. 2차 방정식의 계수를 설정하면 오른쪽에 2차방정식의 포물선 곡선이 그려지므로 다양하게 활용해 볼 수 있다.

3. Y축 절편이 위로 상승하는걸 알 수 있습니다.

수학 함수를 학습 하다보면 전체를 모르고, 지나가는 부분이 많은데 그래프를 자주 그려보면 큰 그림을

그려 볼 수 있으니 꼭 한번씩 그려보면서 학습을 해보세요.

제곱근의 개념, 수학 루트의 개념을 설명하기 위해 제가 직접 작성한글 입니다.

궁금한점은 댓을 남겨주시면 상세하게 설명을 추가하도록 하겠습니다.

https://studyexcel.tistory.com/17

https://studyexcel.tistory.com/23

https://studyexcel.tistory.com/18

https://studyexcel.tistory.com/23

궁금증이나 문의사항은 언제든 댓글 달아주세요